
Ruelle–Pollicott resonances of stochastic systems and a new approach to stochastic bifurcations
Mickaël D. Chekroun
Weizmann Institute of Science & UCLA
Abstract. In this talk, a theory of Ruelle–Pollicott (RP) resonances for systems of stochastic differential equations (SDEs) will be presented, valid for a broad class of stochastic systems. This work extend the theory of RP resonances introduced in the mid-80’s (Ruelle, 1986; Pollicott, 1986) for deterministic systems. Roughly speaking, RP resonances are defined, in the stochastic context, as the eigenvalues of the generator (Kolmogorov operator) of a given stochastic system. By relying on the theory of Markov semigroups and the spectral theory of semigroups, decomposition formulas of correlation functions and power spectral densities (PSDs) in terms of RP resonances will be then presented (Chekroun et al., 2020).
By extending the results of (Chekroun et al., 2014), it will be explained how a notion of reduced RP resonances can be rigorously framed, as soon as the dynamics is partially observed within a reduced state space V. These reduced resonances are obtained from the spectral elements of reduced Markov operators acting on functions of the state space V, and can be estimated from transition matrices. These reduced resonances inform us about the spectral elements of a coarse-grained version of the SDE generator and relate to the generator of the conditional expectation in V, i.e. the optimal reduced system in V obtained by averaging out the contribution of the unobserved variables (Chekroun et al., 2020).
One important byproduct of this approach consists of the diagnosis usefulness that RP resonances offer to characterize dynamics from observations. This is illustrated in the case of a stochastic Hopf bifurcation in (Tantet et al., 2020) and it will be discussed in this talk. In particular it will be shown that such a bifurcation has a clear signature in terms of the geometric organization of the RP resonances in the left half plane. This analysis provides an unambiguous signature of nonlinear oscillations contained in a noisy signal and that can be extracted from time series; a knowledge particularly useful for the modeling of multiscale datasets by networks of stochastic
oscillators such as discussed e.g. in (Chekroun and Kondrashov, 2017; Kondrashov et al., 2018).
Applications to the detection and characterization of such stochastic nonlinear oscillations in a high-dimensional stochastic system, namely the Cane-Zebiak model of El Niño-Southern Oscillation (ENSO) (Cao et al., 2019) subject to noise modeling fast atmospheric fluctuations, will be finally discussed.
About the speaker. The work of Dr. Chekroun is at the confluence zone between the theory of stochastic/nonlinear dynamics and functional analysis (semigroup theory), on one hand, and computational/optimization methods, on the other, with the grand purpose of advancing and developing mathematical concepts, tools, and analysis methods for (i) making progress in the understanding of the mechanisms generating the multiscale patterns occurring in the climate system, and (ii) discovering new dynamical insights for the efficient modeling of these patterns along with their spatio-temporal variability.
Dr. Chekroun’s achievements in the field of applied mathematics to atmospheric and oceanic sciences have placed him among the leaders of this field. Dr. Chekroun is especially renowned for his major original research advancements, including pioneering a new mathematical framework to analyze the global climate’s turbulent variability, demonstrating that fractal structures may co-exist with noise in a generic way, and developing advanced mathematical and computational tools that have provided innovative solutions to predicting extreme atmospheric and oceanic phenomena.
His work at the interface of Mathematics and climate science has been crowned by the several grants awarded by major US governmental agencies including the Department of Energy (DOE), the Mathematical Division of the National Science Foundation (NSF), the Machine Learning, Reasoning and Intelligence program of the Office of Naval Research (ONR), and the Applied and Computational Analysis program of the ONR.
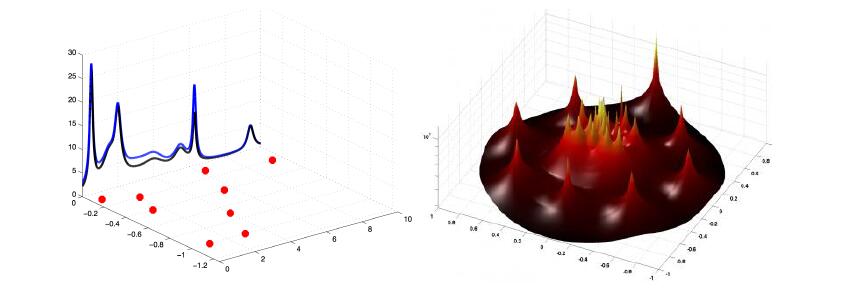
Figure 1: Left panel: The RP resonances are represented by red dots in the horizontal complex plane (generator representation). The imaginary part of the RP resonances corresponds to the location of a peak in the PSD (black curve lying above the imaginary axis) and the real part to its width. In blue is represented a reconstruction of the PSD based on RPs from (Chekroun et al., 2020, Eq. (2.21)); a discrepancy is shown here to emphasize that in practice the RPs are very often only estimated/approximated. Right panel: Reduced RP resonances estimated from numerical integration (time series) of the Jin-Neelin (JN) model of El Niño-Southern Oscillation (ENSO) (Cao et al., 2019) in the propagator representation. In this case, these resonances are obtained as eigenvalues of transition matrices in a reduced state space. The 8 evenly distributed peripheral resonances (sharp peaks) correspond to the quasi-quadriennial oscillation of ENSO as captured by the JN model; see (Chekroun et al., 2014).
References
Cao, Y., M. D. Chekroun, A. Huang, and R. Temam, 2019: Mathematical Analysis of the Jin-Neelin Model of El Nino-Southern-Oscillation. Chinese Annals of Mathematics, Series B, 40 (1), 1–38, doi:10.1007/s11401-018-0115-3.
Chekroun, M., A. Tantet, H. Dijkstra, and J. D. Neelin, 2020: Ruelle-Pollicott Resonances of Stochastic Systems in Reduced State Space. Part I: Theory. J. Stat. Phys., doi:10.1007/s10955-020-02535-x.
Chekroun, M. D., and D. Kondrashov, 2017: Data-adaptive harmonic spectra and multilayer Stuart-Landau models. Chaos, 27 (9), 093 110, doi:10.1063/1.4989400.
Chekroun, M. D., J. D. Neelin, D. Kondrashov, J. C. McWilliams, and M. Ghil, 2014: Rough parameter dependence in climate models: The role of Ruelle-Pollicott resonances. Proc. Natl. Acad. Sci USA, 111 (5), 1684–1690, doi:10.1073/pnas.1321816111.
Kondrashov, D., M. D. Chekroun, and P. Berloff, 2018: Multiscale Stuart-Landau emulators: Application to wind-driven ocean gyres. Fluids, 3 (1), 21, doi:10.3390/fluids3010021.
Pollicott, M., 1986: Meromorphic extensions of generalised zeta functions. Inventiones Mathematicae, 85 (1), 147–164.
Ruelle, D., 1986: Locating resonances for axiom a dynamical systems. Journal of Statistical Physics, 44 (3-4), 281–292.
Tantet, A., M. Chekroun, H. Dijkstra, and J. D. Neelin, 2020: Ruelle-Pollicott Resonances of Stochastic Systems in Reduced State Space. Part II: Stochastic Hopf Bifurcation. J. Stat. Phys., doi:10.1007/s10955-020-02526-y.

